Indices: Detailed Lessons and Examples to Laws of Indices

Indices can be confusing if you do not really understand the meaning and various laws that govern them. In this lesson, I will give the definition of indices, breakdown various laws of Indices, and how to use the law of indices in calculations and simplification.

DEFINITION OF INDICES

Indices is the power of exponent which is raised to a number or variable.

Examples:

1. The short form of writing m x m x m is m3. The letter “m” is called the base while the number 3 is the power, exponent or index.
2. The short form of writing 8x8x8x8x8 is 8⁵

Where the number 8 is the base and the number 5 is the power, exponent or index.

LAWS OF INDICES

1. Multiplication Law

When numbers with equal bases are being multiplied, this powers (indices) are added.

Examples

1. M² X M³

Solution:

M² X M³

Expand the powers of the base (M)

m² = m³ (MxM)

M³ = (M x M x M)

Consider the relationship between the powers

Recall that you were told in this law that when Numbers with equal base are multiplied, their powers (Indices) should be added.

That means the relationship between the powers (2 and 3) is 5

So M² X M³ = M²⁺³ = M⁵

• 9³ x 9⁴

Solution

9³ x 9⁴

Expand the powers of the bases (9)

9³ =  9x9x9

9⁴ = 9x9x9x9

Consider the relationship between the powers

The relationship between the powers (3 and 4) is 7

i.e 3 + 4 = 7

so, 9³⁺⁴ = 9⁷

In general,

a^m x aⁿ = a^m+n  

Note

If two different numbers are multiplied, their powers or index are collected as one group to give the product

EXAMPLE

1. 5³ x 7² x 5⁴ x 7³

Solution

5³ x 7² x 5⁴ x 7³

Collect like terms (Numbers or bases)

5³ x 5⁴ x 7² x 7³

Consider their powers

5³⁺⁴ x 7²⁺³

Ans: 5⁷ x 7⁵

2. Division Law

When dividing numbers with the same base, the divisor is subtracted from the dividend.

EXAMPLE

8⁷ / 8⁵

Solution

8⁷ / 8⁵

8⁷ is divided

8⁵ is divisor

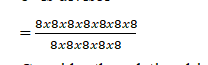
Consider the relationship between the powers.

Since you are solving with the division law, you are to subtract the powers that means, the relationship between the powers (7 and 5) is 2

7 – 5 = 2

So, 8⁷ / 8⁵ = 8^7-5 = 8²

In general

a^k / a^y = a^k-y

3. Power Law

When a number which is raised to a certain power is again raised to another power, it is said to be in powers; you have to multiply the two powers together for the final answer.

EXAMPLE

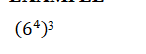
Expand the Numbers: 6⁴ x 6⁴ x 6⁴

= (6x6x6x6) x (6x6x6x6) x (6x6x6x6)

= 6x6x6x6x6x6x6x6x6x6x6x6

= 6¹²

Or

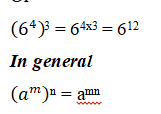
4. Zero Index

When any number is raised to power zero, the result will be 1

EXAMPLES

1. a^m / a^m = a^m-m = a⁰ = 1
2. 3⁴ / 3⁴

By using the division law

3⁴ / 3⁴ = 3^4-4 = 3⁰ – 1

Or

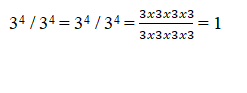
5. NEGATIVE LAW

Any Number raised to a negative index or power equal the reciprocal raised to the positive index.

EXAMPLES

If you have any questions about the laws of indices, let us know in the comment section and if this article is helpful, do well to share it with others by clicking the social media share buttons.