Simplified Lessons on Sequence (A Step by Step Guide)

Many students in secondary schools, as well as higher institutions, do see sequence problems as a very difficult task to tackle.

However, the fear may be because the teacher’s explanation makes it difficult for them to understand but don’t panic. I am going to get you through a step by step approach of eliminating this fear, gather your writing materials and give me your individual attention.

In this lesson, I am going to teach you two set of problems encountered in Sequence. How to write down the number of terms of a sequence when the nth term is given and how to write the nth term when numbers of Sequence are given

Before we get started, let know what Sequence means.

Sequence is a succession of terms in such a way that the terms are related to one another according to a well defined rule e.g 3, 6, 9, 12, 15 …….

You can see in each new term f3 is added to the previous term.

That means the rule is ‘add’ 3’:

Each number is called a term

The nth term of a Sequence is represented by in likewise, the first, second and third terms can be written as T₁, T₂, T₃, respectively.

So let start with examples on the first aspect of Sequence.

Solutions to Sequence Questions

EXAMPLE 1:

A particular term of a Sequence is represented by the formula 3×2ⁿ⁺². What is the sum of the 5th and the 6th terms?

SOLUTION
Step 1: As stated earlier, the nth term of a Sequence is represented by T_n. therefore from the formula given T_n = 3×2ⁿ⁺².

Step 2: n in the formular represent the number of terms i.e n can be 1,2,3,4 etc. the 5th term means that n is 5. So put 5 where you see n in the formula

T₅ = 3×2⁵⁺²            

STEP 3: Add the power of 2 in the formular and multiply by the other term. i.e 2 plus 5

T₅ = 3×2⁷

T₅ = 3×128

You wonder how I got the 128?

N/B: Sum means addition of numbers

Therefore, T₅ + T₆ = 384 + 768

= 1,152

EXAMPLE 2:

The nth term of Sequence is denoted by 3n (2ⁿ-1). Write down the first four terms of the Sequence.

Solution

Step 1: the nth term represented by Tn, Tn = 3n (2ⁿ-1).

The first four term means n = 1,2,3 and 4 respectively

For the first term, put 1 where you see n

That means T₁  = 3×2 (2¹-1)

I hope you remember BODMAS. So we start by solving what is in the bracket

N/B: Any number raise to the power of one gives that number, so 2¹=2

STEP 2:

T₁  = 3×1 (2-1)

T₁  = 3×1 (1)

What is in the bracket is used to multiply what is outside

T₁  = 3×1

Why? 1×1 = 1

For the second term, n = 2

i.e T₂  = 3×2 (2²-1)

as usual we tackle what is in the bracket first

T₂  = 3×2 (4-1)

How did I get 4?

2² = 2×2 = 4

T₂  = 3×2 (3)

Multiply 2 by 3 again

T₂  = 3×6 = 18

Therefore T₂  = 18

For n = 3

Similarly, we substitute 3 for n that means

T₃  = 3×3 (2³-1)

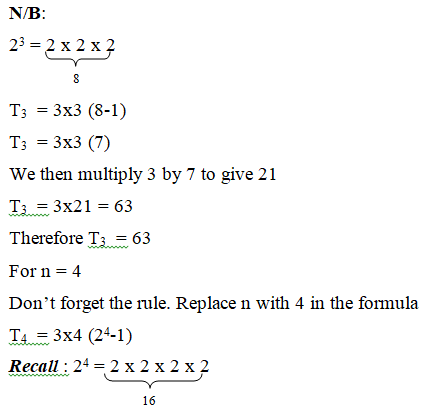
i.e 2 into four places

T₄  = 3×4 (16-1)

T₄  = 3×4 (15)

We multiply 4 by 15 to yield 60

T₄  = 3×60 = 180

Therefore the first four terms are

T₁,T₂,T₃,and T₄

Values which are 3, 18, 63, 180

EXAMPLE 3:

Fine the difference between the 4th and 11th terms of the Sequence whose nth term is 5-n²/2n

SOLUTION

STEP 1: T_n = 5-n²/2n i.e nth term is T_n

The 4th term means that n=4, so put 4 where you see n in the formular

T₄ = 5-4²/2×4

I believe you have not forgotten that 42 = 4×4 = 16

T₄ = 5-16/8 = -11/8

Therefore T₄ = -11/8

Therefore, the 11th term n = 11

T₁₁ = 5-11²/2×11 = 5-11×11/2×11 = 5-121/22

T₁₁ = -11/22

Since we are through with the first set of problem encountered in Sequence let now focus on the Second. Let start by solving some problems for better understanding of what I am talking about.

EXAMPLE 4:

Write down the nth term of the Sequence

9,15,21,27….

SOLUTION

STEP 1: Recall nth term in this lesson means T_n. so you are required to find the formula that will suit the Sequence.

What is the rule in this Sequence?

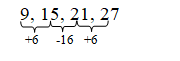
That means the rule is add 6, i.e Each new term is 6 more than the previous term

STEP 2: The first term T₁ = 9

That means

T₁ = 3+6×1 = 3+6 = 9

Similarly, T₂ = 3+6×2 = 3+12 = 15

Again, T3 = 3+6×3 = 3+18 = 21

Therefore, the nth term (T_n) for the Sequence will be

T_n = 3+6_n

So that for number of n, the Tn will give the required number in the Sequence

EXAMPLE 5

Write down the nth term of the Sequence. 51/2, 8, 101/2, 13…..

SOLUTION

STEP 1: what is the rule?

What is the rule in this Sequence?

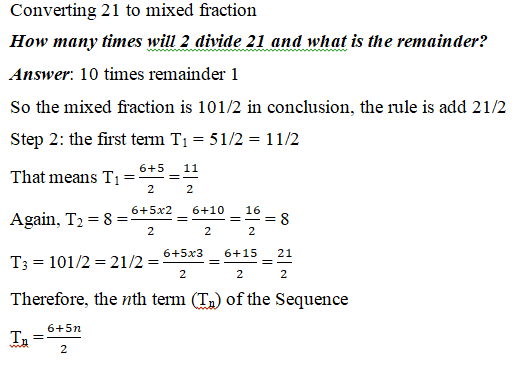
I strongly believe you have no doubt or fear in solving problems involving Sequence.

Remember always to follow the rules in Sequence and the various steps you have learned today. I bet you there will be no obstacle regarding Sequence

It is as easy as that !