Tutorial on the nth Term of A Geometric Progression (G.P.) | The Simplest Method

Some students run away from Geometric Progression problems, simply because they find it difficult to differentiate it from Arithmetic Progression.

They believe the common difference is the same thing as the common ratio so they get tired when solving and they make a lot of mistakes.

In this lesson, I will show you the difference between common difference used in A.P and common ratio used in G.P. and as well give you a breakdown of solution to problems in the nth term of a G.P.

At the end of the lesson, you will come to discover how simple problems involving the nth term of a G.P. are.

A Geometric Progression also known as exponential Sequence) is a Sequence in which any two consecutive terms differ by a constant factor.

The common ration is densted by ‘r’ and the first term ‘a’. but in A.P common difference is used if a set of numbers 6,18,54,162…are given

The common ration =  18/6 = 3, 54/18 = 3, 162/54.

While the common difference is subtraction i.e 18-6, 54-18….

Common ratio is division, since the common ratio ‘r’ is known and the first term ‘a’ is also known, the process of finding the second term is by multiplying the first term by the common ratio.

That is a, ar, ar², ar³…. ar^n-1

Therefore, an nth term of a G.P. is given as

T_n = ar^n-1

N/B: T_n = nth term, r=common ration, a = first term

Put this formula down and also save it in your brain. You will really need it.

Having known some important things about nth term of a G.P. like ho to obtain the common ratio and the formula for nth term of a G.P. let me eliminate your fear of G.P problems by solving some examples.

Hope we are good to go!!

Solutions to Geometric Progression Questions

Example 1: the 6th term of a G.P is 1215. Given that the common ration is 3, find the 9th term.

Solution

In this problem common ratio is r=3, n=6

The 6th term = 1215

Using the formular for the nth term of G.P T_n = ar^n-1 we substitute what is given in order to obtain the first term ‘a’

T₆ = ax3^6-1 = 1215

          ax3⁵ = 1215

rem: 3⁵ = 3x3x3x3x3

Example 2: The third term of a GP is 9 and the fifth term is 16. Find the 4th term.

Solution.

In the above problem given, the third term that is T₃ = 9 and T₅ = 16

We are required to find two equations and then solve them simultaneously.

Using the formular T_n = ar^n-1

T₉ = ar^3-1 = 9

ar² = 9 — (1)

T₅ = ar^5-1 = 16

ar⁴ = 16 — (2)

Divide equation two by 1

 ar⁴/ar² = 16/9

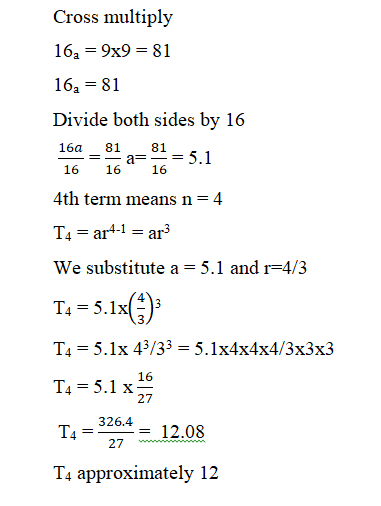
Examples 3: if 3,A,B, 192 are consecutive terms of a GP find the value of A and B.

Solution

In the problem given,

The first term a=3

The second term is A

The third term is B

The fourth term is 192

That means

a=3, T₄ = 192

using the formular for nth term of G.P

T_n = ar^n-1

T₄ = 3xr^4-1 = 192

Multiply 3 by r³

3r³ = 192

Divide both sides by 3

3r³/3 = 192/3

r³ = 64

Take cube rook of both sides

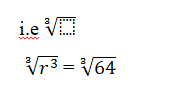
N/B: Cube rook can be express as 1/3 (2) Cube root of a number means a number that can multiply itself three times to give that number e.g 8, the cube rook of 8 is 2 means 2x2x2 = 8 (3) Cube root of 64 = 4

How? 4x4x4 = 64

r^3×1/3  = 4

r = 4

Since we both have gotten a and 8, let solve A and B

Example 4: the first and third term of a GP are 5 and 80, respectively, what is the 4^th term?

Solution

In the problem above

The first term a =5

The third term T₃ = 80

Using the formula

T_n = ar^n-1

T₃ = ar^3-1  = ar² = 80 —– (1)

Put a=5 into equation (1)

5xr² = 80

Multiply 5 by r²

5r² = 80

Divide both sides by 5

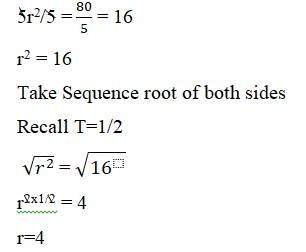
The 4th term, n=4

T₄ = ar^4-1 = ar³

Put a=5 and r=4

T₄ = 5×4³ = 5x4x4x4

T₄ = 5×64

T₄ = 320

Recall: Second Term is A, that is T₂ = A

T₂ = ar^2-1 = A    

A = ar

Substitute a=3 and r=4

A = 3×4 = 12

Therefore A=12

Again, third Term is B

T₃ = ar^3-1 = B

B=ar²

B= 3x(4) = 3x4x4 = 3×16

B = 48

Therefore A=12 and B=48

Example 5:

A G.P has its 3rd and 7th term as 45 and 3645 respectively what is the product of its 2^nd and 4^th term?

Solution

Form the problem

The 3rd term T₃ = 45

The 7th term T₇ = 3645 

Using the formular

T_n = ar^n-1

T₃ = ar^3-1  = 45

ar² = 45 —– (1)

T₇ = ar^7-1  = 3645

ar⁶ = 3645 —– (2)

divide equation 2 by 1

ar⁶/ar² = 3645/45

rxrxrxrxrxr/rxr = 81 How?

Its because rxrxrxr = r⁴

r⁴ = 81

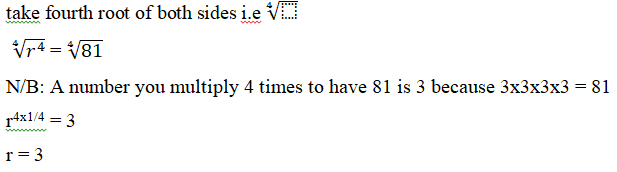
substitute r = 3 into equation 1

ar²= 45

a x (3)² = 45

ax3x3 = 45,axa = 45

9a = 45

Divide both sides by 9

9a/9a = 45/9 a =5

Therefore a = 5 and r =3

And term T₂

T₂ = ar^2-1 = ar

Substitute a = 5 and r=3

T₂ = 5×3 = 15

T₄ = ar^3-1 = ar²

T₄ = 5×3² = 3×3 = 5 x 9

= 45

Product means multiplication so the product of the 2nd and 4th terms is T₂xT₄ = 15×45 = 673

No doubt you have learnt a lot. What you have learned today point to the fact that you can solve as many as possible problems involving nth term of G.P. and that problems involving nth term of G.P are not difficult and should not scare you. I believe the fear has been eliminated.

See:

• Simplest way to Solve indices
• Solution to Sequence Problems

Remember to take note of the formulas for today’s lesson.