How to Solve Sum of Terms in G.P. | Become a Guru

I believe you have familiarized yourself with the nth term of a G.P and you can solve some mind-blogging problems there. If you have done that Wow!

You are on the right track because what you are going to learn today is another phase of G.P but very interesting if you pay attention. Don’t be disturbed you are in the right place.

In today’s lesson, I am going to teach you how to solve problems regarding the sum of nth term of a G.P but you are going to do me a favour.

Get your writing materials and your calculator ready because you are actually going to save some important formulas that will be used throughout the course of this lesson.

I hope you are set how! Ok let’s roll!

The sum of term in any G.P is not a difficult task to overcome.

The general expression for a geometric series is a+ar+ar²+ar³+arn^-1

The sum of the first n terms of a G.P will be

Sn= a+ar+ar²+ar³+arn^-1 ……. + arn^-1

Multiplying Equation 1 by r, will yield

rSn= a+ar+ar²+ar³+ar⁴ ….. arⁿ

subtracting 2 from 1 yields

Sn – rSn = a=arⁿ

Sn (1-r) = a(1-rⁿ)

Divide both sides by (1-r)

Sn(1-r)/(1-r) = a(1-rⁿ)/(1-r)

Therefore Sn = a(1-rⁿ/1-r …… (1)

This formula is used for finding the sum of n terms of a G.P where r is approximately 1

Multiply the formular by -1 i.e both the numerator and the denominator

Sn= -1 a(1-rⁿ)/-1(1-r)

a(-1-(-rⁿ)/-1(1-r)

Sn = a(-1+rⁿ/-1+r

Rearranging what is in the brackets yields

Sn = a(rⁿ-1)/r-1…… (4)

Equation 4 is more confident when r >1

So in essence, save this

Sn = a(1-rn)/1-r, r < 1

For point 1 am trying to highlight here get clearer to you, I think we need to solve some problems right! Yes    !

Solutions to Sum of Terms in GP

Example 1:

The third term of a G.P is 12 and the first term is 48. Find the sum of the first 11 terms

Solution

The first term a = 48

The third term T₃ = 12

Using the formula for nth term

T_n = ar^n-1

T₃ = ar²=12

 ar²= 12 —– (1)

put a = 48 into equation 1

48r² = 12

Example 2: is the second and fourth term of G.P are 8 and 3r respectively. Find the sum of the first nine terms.

Solution

The second term T₂ = 8

The fourth term T₄ = 32

Using the nth term formula

T_n = ar^n-1

T_r = ar^2-1

ar = 8 —— (1)

T₄ = ar^4-1

ar3 = 32 —- (2)

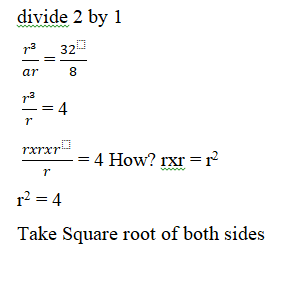
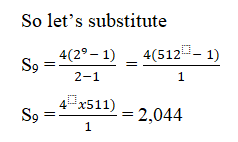
Therefore the sum of the first nine terms is 2,044.

Example 3: if 7 and 189 are the first and fourth term of a G.P respectively, find the sum of the first three terms of the Progression.

Solution

The first term a=7

Fourth term T₄ = 189

T₄ = ar^4-1

ar³ = 189 —– (1)

put a=7 in the equation 1

7xr³ = 189 How? 7 multiplied by r³ is 7r³

7r³ = 189

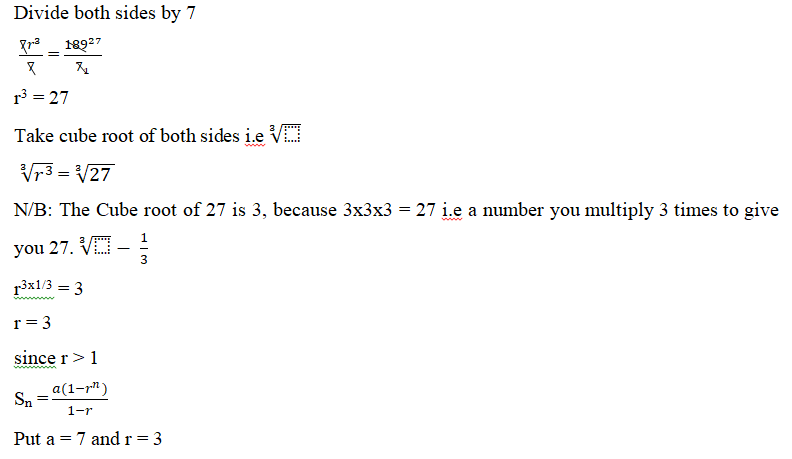
The sum of the first three term five

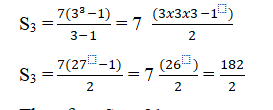
Therefore S₃ = 91

Example 4: Geometric Progression has the second term as 9 and the fourth term as 81. Find the sum of the first four terms.

Solution

As stated from the problem

The second term T₂ = 9

The fourth term T₄= 81

Using the formula for nth term of a G.P i.e T_n = ar^n-1

Using the second term, put 2 where you see n

T₂ = ar^2-1 = ar¹ = ar

ar= 9 —– (1)

Again for the fourth term, put 4 where you see n

T₄ = ar^4-1 = ar ³

ar ³ = 81 —– (2)

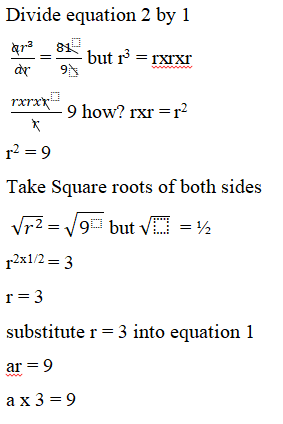
I believe you really understood today’s lesson sum of terms of Geometric Progression is not as cumbersome as they said right?

Because you can solve many problems in sum of G.P with the knowledge you have obtained today.