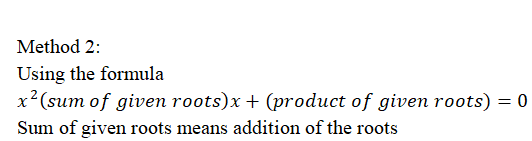Do you sometimes panic about how quadratic equation roots are used to form a quadratic equation? Or have you stumbled into one problem but unable to solve it?
If you have, worry no more because I am going to make it simple for you. If you have already studied this topic or taught by a friend or a teacher but seem not to understand, probably it may be because they did not unveil the secret behind it to your understanding or did not use the required methods to teach you.
Here, I am going to give you an explicit explanation on how to solve it but first let’s know what a quadratic equation means.
A quadratic equation is an expression of the form ax2+bx+c=0 in which a,b,c are numerals and also the highest power of x is 2 and that the power x will neither by fractions nor negatives.
When the roots of a particular quadratic equation are given and the equation whose roots are required to find.
There are two methods to be used to obtain the needed equation.
I am going to teach you the two methods in this lesson.
Method 1:
This method says “Subtract each root from x an equate to zero in turns”
Method 2:
This method involves the use of the formula i.e x2(sum of given roots ) x +(product of given roots) = 0
This means that you have to add the root together and also multiply the roots before you substitute it into the formula
Having known the two methods, let,s start by solving problems using the methods listed above.
Example 1:
Construct a quadratic equation given the roots
-4 and -2/3
Solution
Method 1
The roots are -4 and -2/3
This means that x = -4 and
x = -2/3
Subtract each root from x and equate to zero in turns.
This means
x-(-4) and x-(-2/3)
up next! Equate to zero
x-(-4) = 0 and x-(-2/3)
let open the bracket by multiplying what is outside with what is inside
N/B: -x- = +
+x- = –
+x+ = +
-x+ = –
x + 4 = 0 and x + 2/3 = 0
bracket them and equate to zero
(x+4) (x+2/3) = 0
Open the bracket . i.e
x X x + x^x 2/3 + 4x x^ + 4×2/3 = 0
x^2 + 2x/3 4x+ 8/3=0
Multiply through by 3, to eliminate the denominator (to clear the factor)
3x^2 + 6x^2/3_1 +3xX4x+ 3X 24/3=0
3x^2+ 6x^2/3_1 +12x+ 24/3=0
Divide through
3x^2+ 2x+12x+ 8=0
Add the middle terms
3x^2+14x+ 8=0
Therefore the quadratic equation is
3x^2+14x+ 8=0
Method 2:
Using the formula
x^2 (sum of given roots)x+(product of given roots)=0
Sum of given roots means addition of the roots
-4 + ((-2)/3)
But + x – = –
-4 (-2)/3 = (-4 x 3)/3
(-3x-4-2)/3 = (-12-2)/3 = (-14)/3
Product of given roots means multiplication of the roots
That means -4x -(-2)/3=(-4 x-2)/3
Again, – x – = +
= (+8)/3
Substitute the sum and product of roots into the formula
x^2-((-14)/3)x +(8/3)=0
But – x – = +
“x” ^”2″ “+” (“14″ /”3″ )”x +” “8” /”3″ “=0”
Multiply through by 3 to clear the fraction
3 x x^2+3 x 14x/3+3x(8/3)=0
3x^2+(42^14 x)/3_1 +24^8/3_1 =0
Divide through
3x^2+ 14x+8=0
Therefore the quadratic equation is
3x^2+14x+ 8=0
Read Also:
- How to Solve nth Term of G.P
- Simplest Way to Solve Simultaneous Equation
- How to Solve Equation Involving Fractions
- Sum of Term in G.P
- The best way to Solve Sequence
- How to Solve Quadratic Equation by Factorization
Example 2:
Construct a quadratic equation given the roots -1/2 and 3/2
Solution
Method 1:
The roots are -1/2 and 3/2
That mean x=(-1)/2 and x= 3/2^
Subtract each roots from x^and equate to zero in turns
x-((-1)/2)and (x-3/2)
Since – x – = +
(x+1/2)and (x (-3)/2)
Equate to zero
(x+1/2)=0 and (x- 3/2) = 0
This means
x+x+x x (-3)/2+ 1/2 x x+ 1/2 x (-3)/2=0
x^2+((-3x)/2)+ x/2 + (-3)/4=0
Remove the bracket
x^2-3x/2)+ x/2- 3/4=0
Multiply through by the L.C.M of 2 and 4 which is 4 to clear the fraction
x^2 (-3x)/2+ x/2- 3/4=0
4xx^2- 4x3x/2+ 4xx/2- 4×3/4=0
4x^2- (12^6 x)/2_1 + (4^2 x)/2_1 – 12^3/4=0
Divide through (the fraction)
4x^2-4x-3=0
Therefore the quadratic equation is
4x^2-4x-3=0
Method 2:
Using the formula
x^2 (sum of given roots)x+(product of given roots)=0
Sum of given roots = (-1)/2+ 3/2
The L.C.M of the denominator is 2, since the denominator are the same, simply add the numerators
(-1×3)/2+ 2/2
Product of given roots = (-1)/2 X 3/2
Multiply the numerators and the denominators. That means
(-1×3)/2×2= (-3)/4
Substitute the sum and product of roots into the formula
x^2- (2/2)x+((-3)/4) = 0
Open the bracket by multiplying what is outside with what is inside
x^2- 2x/2+(-3)/4) = 0
Multiply through by the L.C.M 4 to clear the bracket
4xx^2-4x2x/2-(-4×3)/4=0
Divide through (the fraction)
4x^2-4x-3=0
Therefore the quadratic equation is
4x^2-4x-3=0
Example
Construct a quadratic equation whose roots are ½ and 3/2
Solution
Method 1:
The roots are ½ and 3/2
That means x^ =1/2 and x=3/2
Subtract each roots from x and equate to zero in turns
(x-1/2)and (x-3/2)
Let equate to zero
(x-1/2)and (x-3/2) = 0
Let multiply through
x x x+x (-3)/2+ (-1)/2 x x+ (-1)/2 x (-3)/2 = 0
x^2+((-3x)/2)+ ((-x)/2)+ 3/4 = 0
N/B: -1xx = -x and – x – = +
Removing the bracket yield
x^2-3x/2- x/2+ 3/4 = 0
Multiply through by the L.C.M of 2 and 4 which is 4
4xx^2-4x 3x/2- 4x x/2+ 4x 3/4 = 0
4x^2 (-12x)/2- 4x/2+ 12/4 = 0
Divide through (the fraction)
4x^2-(12^6 x)/2_1 – (4^2 x)/2_1 + 12^3/4_1 = 0
4x^2-6x-2x+3=0
Add the middle terms
4x^2-8x+3=0
Therefore the quadratic equation is
4x^2-8x+3=0
Method 2:
Using the formula
x^2 (sum of given roots)x+(product of given roots)=0
Sum of given roots = ½ + 3/2
Since the L.C.M of the denominators are the same, we add the numerators
(1+3)/2= 4/2
Product of given roots = 1/2 x 3/2 = 3/4
Let substitute what we have gotten into the formula
x^2 (4/2)x+ 3/4=0
Open the bracket
x^2 (-4x)/2+ 3/4=0
Multiply through by the L.C.M of the denominator which is 4
4xx^2-4x4x/2+ 4×3/4=0
4x^2-(16^8 x)/2_1 + 12^3/4_1 =0
Divide the fractions
4x^2-8x+ 3=0
Therefore the quadratic equation is
4x^2-8x+ 3=0
In conclusion, I hope you have been able to clear your doubt on the topic. With the methods we have used in generating quadratic equations with given roots, you can tackle a problem regarding construction of quadratic equation when the roots are given. Just note the steps involved.