Here Is a Tutorial on How to Solve Equation Involving Fractions

Equations involving fractions is sometimes one of the challenging problems students face. Reason being that this fractions sometimes lead to a quadratic equation while other lead to a linear equation.

Due to this they term it a “challenging problem”. However, the challenge they face here is real but thanks to God, I am here to put a light to this ever disturbing problem they encounter in this topic.

The point to be noted about this topic is that you need to follow the needed steps, if it leads to quadratic equation, you solve it using any of the methods of solving quadratic equation. If it results in a linear equation, you solve it by collection of like terms.

Having known the two most important point about equations involving fractions, let see how we can tackle, some problems.

Solutions To Equations Involving Fractions

Example 1:

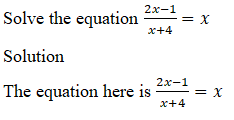
Cross multiply

2x – 1 (x + 4)

Open the bracket in the right hand side

2x – 1 = x² + 4x    

Collect like terms

-1 = x²  + 4x – 2x

Take the constant to the right hand side, and equate it to zero

x²  + 4x – 2x  + 1 

Subtract the middle term

x² i.e 4x – 2x = -2x

x²  + 4x – 2x  + 1 = 0

This means the fraction has led to a quadratic equation so let solve it using factorization method

Multiply the first term with the last term i.e

The method term is 2x

Obtain two factors whose sum will give 2x and the product will yield

The factors are x and x replace the middle term 2x by the two factors x and x

Multiply the numerator

6x/x + 21/7 = 3x²

Divide through (Fractions)

6+7x-6=0

We now have a quadratic equation we multiply the first and last terms as usual

3x² x -6= -18x²

The middle term is ­-7x

The two factors are -9x and 2x

So we replace -7x with -9x and 2x

(3x²-9x) + (2x-6) = 0

The common terms are 3x and 2

3x(x-3) + 2(x-3)=0

(x-3) (3x+2)=0

Separate them and equate to zero to solve for the two values of x

(x-3) = 0 and (3x+2) = 0

x – 3 = 0      3x + 2 = 0

x = 3           3x/3 = -2/3

x = 3 or -2/3

Example 3

Solve the equation 7/2x+5 -3/x+5 = 0

Solution

The equation is 7/2x+5 – 3/x+5 = 0

The L.C.M of the is (2x+5) (x+5)

Clear the fraction by multiplying each of them by the L.C.M

(2x+5) (x+5)

(2x+5) (x+5)x 7/15 – 3/x+5 x (2x+5)

We now have a linear equation

7(x+5)-3 (2x+5) = 0

7x+35-6x-15=0

7x-6x+35-15 = 0

x+20=0

x = -20

Recommended:

• How to Solve nth Term of G.P
• Sum of Term in G.P
• The best way to Solve Sequence
• How to Solve Quadratic Equation by Factorization

Example 4:

Solve the equation x-5=4/x-5

Solution

The equation is x-5 = 4/x-5

Multiply through by the L.C.M x-5

(x-5) (x-5) = 4/x-5 x (x-5)

(x-5) (x-) = 4

Open the bracket

x x x + x x -5 + -5 x x + -5x-5 = 4

x²-5x-5x+25=4

x²-10x+25=4

Take 4 to the left hand side of the equation and equate to zero

x²-10x+25-4=0

x²-10x+21=0

The fraction has resulted in a quadratic equation, so we need to solve it by using factorization method

x²-10x+21=0

multiply the first and the last term

x² x 21=21x²

The middle term is -10x

Two factors whose sum gives ­-10x and product gives 21x²

The two factors are -7x and -3x

Replace the middle term with the two factors i.e

-10x with -7x and -3x

x²-7x – 3x +21=0

(x²-7x) –(3x+21)=0

x(x-7) -3 (x-7)=0

since we have two (x-7), we take one

(x-7) (x-3)= 0

x-7 = 0 and x-3=0

x=7 or x = 3

Example 5:

Solve the equation

½ (x-1) -1/4 (3-x) = 2

Solution

The equation is

(x-1)/2 – (3-x)/4 = 2

Then multiply the both sides of the equation by the L.C.M of the denominator, which is 4

4(x-1)/2 – 4(3-x)/4 = 4 x 2

2(x-y) –(3-x) = 8

Let open the bracket

2x-2-3+x=8

2x+x-2-3= 8

3x – 5 = 8

Collect like terms

3x = 8+ 5

3x/3 = 13/3

x = 13/3

Conclusion

With the solution we have provided to the problems today, answers you can tackle any problem involving equations with fractions. The various steps I laid down are enough for you to get along with problems on this topic.